Centar za edukaciju-BiH

Predmet:Zanimljive krive

---

srcolike krive

---

Predmet:Re: Zanimljive krive

---

Polarni koordinatni sistem je sistem koordinata gdje je pozicija tačke T određena njenom udaljenošću od jedne fiksne tačke R, ishodišta, zajedno sa uglom koji duž RT formira sa jednom fiksnom polupravom. Ishodište R se naziva pol, rastojanje RT naziva se radijus vektor (r), fiksna poluprava naziva se polarna osa (x-osa).


Ugao φ između polarne ose i radijus vektora naziva se vektorski ugao, ili polarni ugao, azimut, amplituda, pa i anomalija. Pozitivan smjer ugla φ je obrnut smjeru kazaljke na satu, negativna vrijednost je u smjeru kazaljke na satu. Koordinate tačke T su uređen par brojeva (r,φ). Polarne koordinate u ravni su korisne za sisteme sa centralnom simetrijom.

Polarni koordinatni sistem je specijalni oblik cilindričnog koordinatnog sistema kad se ne posmatra vertikalna koordinata z.

---

Predmet:Re: Zanimljive krive

---

Kardioida je dobila ime po grckoj rijeci e καρδία "srce"). . Nastaje tako sto pratimo tacku na kruznici koja se kotrlja oko fiksnog kruga istog radijusa. Specijalan slucaj je epicikloide kada obe kruznice imaju isti poluprecnik.

Kriva data u polarnim koordinatama
r=a(1-cosθ)
moze se zapisati i na sljedeci nacin
r=2b(1-cosθ) jer je a=2b

u Dekartovim koordinatama
(x²+y²+ax)²=a²(x²+y²) ili
(x²+y²)-2ax(x²+y²)-a²b_²=0

Parametarska jednacina
x=acost(1-cost)
y=asint(1-cost)

u kompleksnoj ravni to je
z=a(2e^it-e^2it)

Kardioida je algebarska kriva cetvrtog reda.
Ima samo jedan siljak.

Duzina jednoga kraka kardioide zadane formulom
    r=a(1-cosθ)
data je sa l=8a

Povrsina jednoga dijela kardioide je:
P=3a2π/2

Duzina luka
S=8asin2(t/4)

Zakrivljenost
K=3esc(t/2)

Tangentni ugao
ø=3t/2

---

Predmet:Re: Zanimljive krive

---

cvjetne krive

---

Predmet:Re: Zanimljive krive

---

mislim da treba
r = a |sin nθ|
sinus i cosinus mogu da budu i negativni, a r ne moze

Predmet:Re: Zanimljive krive

---

Kako na najjednostavniji nacin nacrtati srcolike krive


U najjednostavnijem slucaju, srce je formirano nad kvadratom. Dva polu-kruga leze na bocnim stranama.


Srce nastalo tako sto su nacrtana 2 polugruga nad jednom stranicom trougla

Srcolika kriva koju cine 3 polukruga

Imamo dva jednakokraka trougla sa zajednickom osnovicom. Nad kracima trougla manje povrsine konstruisemo 2 polukruga. Dobijamo srcoliku krivu.


Nacrtamo 2 kruznice koje se dodiruju i njihovu zajednicku tangentu. Zatim jos po jednu vanjsku tangentu iz jedne tacke, koja se nalazi na prvoj tangenti. Dobicemo srcoliku krivu.



Nacrtati kvadrat, zatim 4 kruznice ciji su centri vrhoci kvadrata, a poluprecnik polovina duzine stranice kvadrata. Nastaje srcolika kriva


Nacrtano elipsu koju rotiramo za 45^ou oba smjera. Te 2 elipse postavimo tako da se sijeku. Ove 2 elipse formiraju 2 srca


Nacrtati grafik funkcije f(x)=sinx za 0<x<π/2. Zatim ga rotirati za 90^o u oba smjera. Ove dvije slike postaviti tako da imaju jednu zajednicku tacku (vrh). Nacrtati 2 polukruga na dio x ose koju odsjecaju ove 2 krive.


Nacrtati grafik funkvije f (x) = sin (x) na -π / 2 <x <π / 2.
rotirati krivu za 90^ou oba smjera. Postaviti ove 2 krive tako da one i jedna duz cine trougao. Nad stranicom koju cini duz nacrtati 2 polukruga.

---

Predmet:Re: Zanimljive krive

---

Hamnet Holditch (1800-1867) stredinom XIX vijeka bio je dekan na Caius College, Cambridge. Interesantna je njegova teorema objavljen 1858. god.

Zamislimo zatvorenu konveksnu krivu.Povucimo duz koja spaja dvije razlicite tacke krive. Napomena ova duz mora imati konstantnu duzinu. Duz podijelimo na 2 segmenta p i q. Ako se ova duz pomjera po zadanoj krivoj C₁ tacka na duzi, koja je dijeli na segmente p i q, opisuje zatvorenu krivu C₂. Ona je unutar zadane krive. Podrucje izmedju krivih C ₁ i C₂ ima povrsinu:

P=πpq

Zadivljujuca cinjenica je ta sto ova povrsina ne zavisi od povrsine krive C₁.

Za krug radijusa R to je krug.

r=(R²-pq)^1/2

---

Predmet:Re: Zanimljive krive

---

ohan Bernuli je 1696. godine postavio jedno interesantno pitanje bratu Jakobu:

“ Koja je ta kriva kojom ce tijelo uz uticaj gravitacione sile stici od tacke A do nize tacke B za najkrace vrijeme?”

Zadatak su od grcke rijeci brachistochrone (koje znaci najkrace vrijeme), nazvali Brahistokronovim problemom. Kod rjesavanja problema dosli su i do zakljucka, da kad pustimo tijelo iz bilo koje tacke ove krive, tijelu ce uvijek trebati istovremeni period da bi stiglo do najnize tacke te krive. Jakob je tacno odgovorio : “Rjesenje je cikloida! “



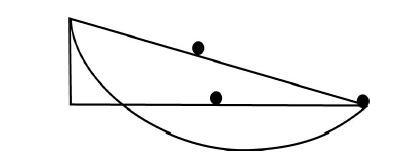
edna od najpoznatijih krivi u istoriji matematike je cikloida. Cikloidu je prvi proucavao de Kusu, kasnije Mersen. Kriva je dobila ime po Galileju 1599. godine. On je pokusao da odredi povrsinu ispod jednog luka, ali bezuspjesno. Matematicki metod nije uspio da pronadje, te je izrezao komadice metala u obliku povrsine ispod cikloide i uporedjivao tezinu sa tezinom kruga koji generise cikloidu. Dosao je do rezultata da je cikloida teza oko tri puta od kruga, ali je on odbio da prihvati ovaj rezultat jer je vjerovao da odnos izmedju ove dvije tezine, treba da bude iracionalan. Ispostavilo se da je Galilejev eksperimenat zaista dao tacan rezultat.

Roberval je 1628. godine odredio povrsinu cikloide koristeci novi metod “beskonačno malih”, koji je razvijen od strane Kavalijerija , Ferma i Dekarta, kao i Robervala, medjutim svaki od njih je pronasao drugaciji metod za povlacenje tangente na ovu krivu. Toriceli, ucenik Galileja je 1644. godine objavio svoje otkrice o povrsinama i tangentama cikloida.

Cikloida je, u tom dobu, bila jedna od najpopularnijih problema matematike, mnogi sporovi i ljubomore su nastale vezani za nju, zato je postala poznata po imenu “Helena geometricara”. U skladu sa Arhimedovom tradicijom, Hajgens, Lajbnic i Johan Bernuli su trazili posebne dojelove regiona cikloide cije su povrsine jednostavnog pravolinijskog oblika.


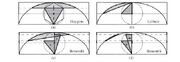
va slika ilustruje njihovu zajednicku stavku. Svaki cikloidni luk je opisan jednim pravougaonikom koji je prepolovljen po horizontalnoj srednjoj liniji, sa kotrljajucim krugom u centru.

Godine 1658. Hajgens je pokazao da dio cikloide odsjecen isprekidanom linijom na slici (a), koja prepolovljava gornju polovinu pravougaonika, ima povrsinu jednaku polovini upisanog pravilnog sestougla u kotrljajuci krug, ili ekvivalentno - jednaka povrsini osjencanog jednakostranicnog trougla upisanog u isti krug.

1678, Lajbnic je dokazao da segment cikloida na slici (b) ima istu povrsinu kao i osjencani pravougli trougao, ciji su kraci jednaki poluprecniku kruga.

1699, Bernuli je prosirio oba rezultata, koristeci dvije horizontalne isprekidane linije, jednako udaljene od srednje i gornje linije kao sto je na slici (c) i (d).

On je dokazao da je povrsina segmenta cikloida na slici (c) zbir povrsina dva osjencana pravougla trougla, dok je manji segment cikloide na slici (d) predstavlja razliku povrsina pravouglih trougla. Dijagram na slici (c) se pojavljuje na naslovnim stranicama sva cetiri toma sabrana djela Bernulija.

---

Predmet:Re: Zanimljive krive

---

Kinematicki metod opisivanja krive potice iz mehanike, a opisuje krivu kao putanju po kojoj se krece tacka koja slijedi odredjene zakone fizike.



ata kruznica r poluprecnika a, koja se kotrlja po x osi. Tacka sa njene periferije pri tom kotrljanju opisuje cikloidu.

Neka je tacka O (koordinatni pocetak) pocetni polozaj tacke A (na slici M) koja opisuje cikloidu

t je ugao za koji se kruznica obrnula ( ugao ACB na slici ugao MCQ)

a je poluprecnik kruznice (na slici obiljezen sa r)

Vazi, jer je kotrljanje bez klizanja.

AB=OB=at

Za pretpostavljeni polozaj tacke A, koordinate su

x = OB - OE
y = CB - CE
E je tacka koja je na slici obiljezena sa N.

Sa slike vidimo da vazi
AE = a sint
CE =a cost
Odakle se dobijaju parametarske jednacine cikloide

x=a(t- cost)

y= a(1 - cos t )

Jedan svod cikloide je dio krive koju posmatrana tacka opisuje sa jednim obrtajem kruga.

---

Predmet:Re: Zanimljive krive

---

Duzina luka jednog svoda cikloide je 8a, gde je a poluprecnik kruga.

Duzina luka krive je

---