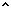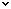Predmet:Re: Zadaci iz geometrije
Zadatak 7
Analiza

Dato je duz a+b+c i uglovi α i β
Neka je duz MN duzine a+b+c. Trouglovi AMC i BNC su jednakokraki.
Iz cinjenice da je spoljasnji ugao jednak zbiru dva unutrasnja nesusjedna proizlazi da su uglovi AMC i MCA jednaki α/2. Slicno uglovi BNC i NCB iznose β/2.
Kako imamo duz MN i uglove AMC i BNC mozemo konstruisati trougao MNC. ( trougao je odredjen ako je zadana jedna njegova stranica i dva ugla na toj stranici).
Konstrukcija

Nacrtamo polupravu Mx. Od njenog pocetka (tacka M) nanesemo duz a+b+c i dobijemo tacku N. U tackama M ( N) nanesemo uglove α/2 i β/2. na taj nacin dobili smo jos dvije poluprave My i Nz takve da je
My∩Nz)={c}.
Na ovaj nacin konstruisali smo trougao MNC.
Tacke A i B nalazimo tako sto konstruisemo simetrale stranica MC i NC. U presjeku sa duzi MN nalaze se tacke A i B.

"Ne treba se stidjeti nikakvog posla, pa čak ni onog najprljavijeg; treba se stidjeti samo besposlenog života." - Tolstoj
Ovaj post je ureden
2
puta. Posljednja izmjena 11.10.2010 07:27 od strane roza.